Hysteresis Loop Characteristic
A hysteresis loop reveals a magnet’s essential characteristic of nonlinear relationship between magnetization M and applied magnetic field H. The hysteresis loop is also known as a hysteresis curve. Since the magnetic induction intensity B is related to M and H (as shown in equations 1 and 2 [1]), we may see M-H loop, B-H loop, M-H curve, B-H curve.
In the CGS unit system, B = H + 4πM (1)
In the SI unit system, B = μ0(H+M) (2)
where the vacuum permeability μ0 is a physical constant, 4π×10^-7 H/m.
At the origin of the M-H hysteresis loop of Figure 1, the magnet is in unmagnetized state. Microscopically, the magnet has many spontaneously magnetized domains, and the magnetic domains are randomly oriented. As the applied field starts to increase, the magnetic domains move and rotate along the magnetization direction. When it sufficiently exceeds the saturation magnetization Ms, the magnet is fully magnetized to saturated state. When it turns down to zero, magnetization remains the remanence Mr, Mr ≤ Ms. When the applied field turns reverse, the magnet will be demagnetized. The intrinsic coercivity Hci is the point where the magnetization is reduced to zero. If the reverse field is high enough, the magnet will achieve Ms again in the reverse direction.
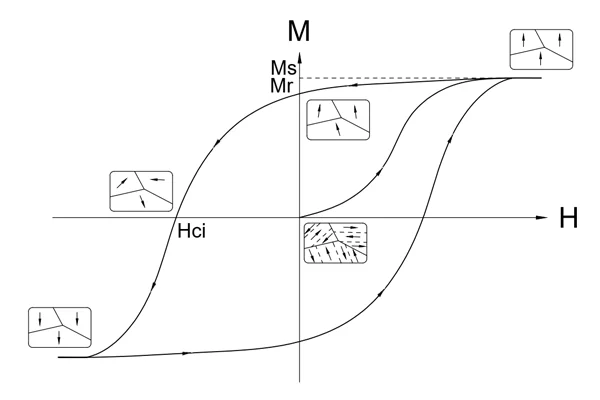
Hard Magnet Feature vs. Soft Magnet Feature
Hard magnets have broad and square M-H, B-H loops. As they remain in magnetized state when the applied field is removed, they are also known as permanent magnets. Hard magnet engineers aim to develop higher remanence, higher coercivity, higher maximum energy product, etc.
Soft magnets have thin and narrow M-H, B-H loops. As they lose their magnetization soon when the magnetizing field is removed, they are also known as temporary magnets. Soft magnet engineers aim to develop higher initial permeability, higher saturation magnetic flux density, smaller coercivity, etc.
References
[2] J.M.D. Coey, Magnetism and Magnetic Materials, Cambridge University Press & Peking University Press, 2014.